(CL∙AQ∙BD)/(LB∙CQ∙DA)=1. (1)
Но и AB – секущая для Δ СQL. Можно применить ту же теорему:
(AQ∙CB∙LD)/(AC∙BL∙DQ)=1. (2)
Приравняв (1) и (2), имеем:
CL/CQ=(CB∙LD∙DA)/(AC∙DQ∙BD). (3)
EL || QA => Δ EDL подобен Δ ADQ и (LD/DQ)=(DE/DA). (4)
Тогда (3) можно записать в виде:
CL/CQ=(CB∙DE∙DA)/(AC∙DA∙BD)=(CB∙DE)/(AC∙BD). (5)
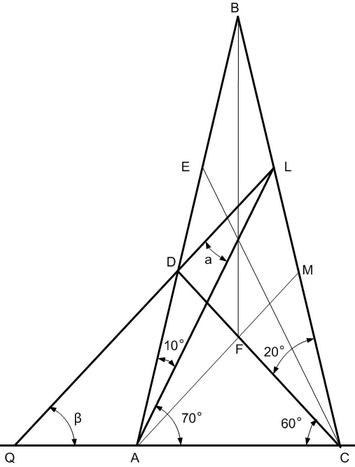
Проведем через точку F прямую AM.
Заметим, что Δ ACF и Δ DMF равносторонние, а Δ BCD равнобедренный.
В Δ BCD биссектриса BF делит СD в отношении
DF/FC=BD/BC=BD/AB (6),
а биссектриса CE делит BD в отношении
DE/BE=CD/BC=BD/BC=BD/AB (7).
Учитывая (6) и (7), а также, что BD=CD, получим: DE=DF=DM.
Тогда DE/AC=DM/AC=BD/AB=BD/CB, т.е. DE/AC=BD/CB (8).
Рассматривая (5) совместно с (8), получаем: СQ/CL=1,
т.е. Δ CLQ равнобедренный. Угол при вершине C=80˚,
углы β при основании LQ равны 50˚.
^ELQ как накрестлежащий к ^LQC тоже равен β.
^ELA как накрестлежащий к ^LAC = 70˚.
α+β=70˚. Итак, α=70˚-β= 20˚.